Il existe 2 grandes méthodes de chiffrement asymétrique : RSA et ECDSA.
RSA se base sur des calculs modulaires de nombres premiers. Pour faire simple, le principe se base sur le produit de 2 nombres premiers, n=p.q. Quand on connaît p et q, il est trivial de calculer n. Mais quand on ne connaît que n, alors sa factorisation prend « un certain temps » (comme dirait Fernand Raynaud). Le tout est que ce temps-là soit suffisamment long…
Il existe plusieurs méthodes de cryptanalyse. La première, déjà évoquée, consiste à décomposer n en facteurs premiers. Si ce nombre est très grand, alors le temps de sa décomposition le sera également. Sauf si ces nombres en jeu répondent à quelques propriétés mathématiques complexes ! Par exemple, si (p-1)/2 n’est pas premier, alors sa factorisation se calculera rapidement à l’aide de l’algorithme « p-1 » de Pollard. Une autre approche consiste à se rappeler que la vérification de la primalité d’un grand nombre n’est pas exacte mais probabiliste (i.e. on a une toute toute petite probabilité de se tromper : voir algorithme de Miller-Rabin). Autre exemple plus vicieux : si p et q ne sont pas calculés de manière réellement aléatoire, alors il est possible de recréer les conditions préalables à la détermination « pseudo-aléatoire » de p et q, et ainsi de recalculer ces 2 nombres de base ! C’est pour cette raison qu’il est fortement déconseillé (voire interdit) d’utiliser des PC virtuels (cloud et compagnie), pour lesquels le générateur d’aléa n’est pas fiable. Un bon générateur d’aléa va se baser sur les événements physiques se produisant sur un ordinateur (variations de tension d’entrée, accès au disque dur…) : un PC virtuel et sans disque dur se retrouvera toujours dans le même état exact au bout de n secondes après chaque reboot. Bref, certaines méthodes peuvent permettre de deviner tout ou partie des multiplicateurs p et q.
La seconde méthode de cryptanalyse consiste à faire déchiffrer quelques données bien spécifiques, tout en chronométrant le temps passé. À partir de ces informations, il devient possible de calculer les 2 primaires p et q. Le proof of concept a été réalisé en 1998 et a nécessité environ 1 million de paquets réseau (c’est une discussion assez verbeuse mais habituelle) sur un réseau local et 2 heures de calculs, pour une clef de 1024 bits. Sur un réseau public, cela aurait demandé plus de temps et plus de paquets. Et depuis 1998, les systèmes se sont améliorés… La méthode RSA blinding permet d’annuler ce type d’attaque (on rajoute une constante lors des calculs de chiffrement et de déchiffrement, ce qui déforme le chronométrage des opérations).
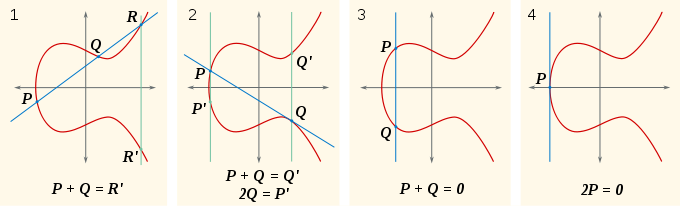
ECDSA se base sur des courbes elliptiques. Le principe est similaire, à base de 2 nombres sur la courbe dont on calcule le produit scalaire (3e point sur la courbe). Les méthodes de cryptanalyse se basent sur de l’observation indirecte, par exemple le temps passé, la consommation électrique, le rayonnement électromagnétique (appelés canaux auxiliaires ou canaux cachés) lors du calcul de ce produit scalaire.
La grande différence entre ces deux méthodes est l’opération mathématique mise en œuvre. RSA se base sur de la factorisation, et ECDSA se base sur des logarithmes discrets. La taille minimale de la clef pour éviter une attaque par force brute est très différente : aujourd’hui on parle de clef RSA de 2048 bits pour assurer une bonne sécurisation, tandis que la clef ECC (Elliptic Curve Cryptography) minimale sera de 256 bits. Une grande taille de clef demande davantage de puissance de calcul !